逐层排序二叉树所需的最少操作数目
0
Word Count: 567(words)
Read Count: 2(minutes)
题目:
给你一个 值互不相同 的二叉树的根节点 root 。
在一步操作中,你可以选择 同一层 上任意两个节点,交换这两个节点的值。
返回每一层按 严格递增顺序 排序所需的最少操作数目。
节点的 层数 是该节点和根节点之间的路径的边数。
1
2
3
4
5
6
7
8
| 输入:root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出:3
解释:
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作,所以返回 3 。
可以证明 3 是需要的最少操作数目。
|
思路:
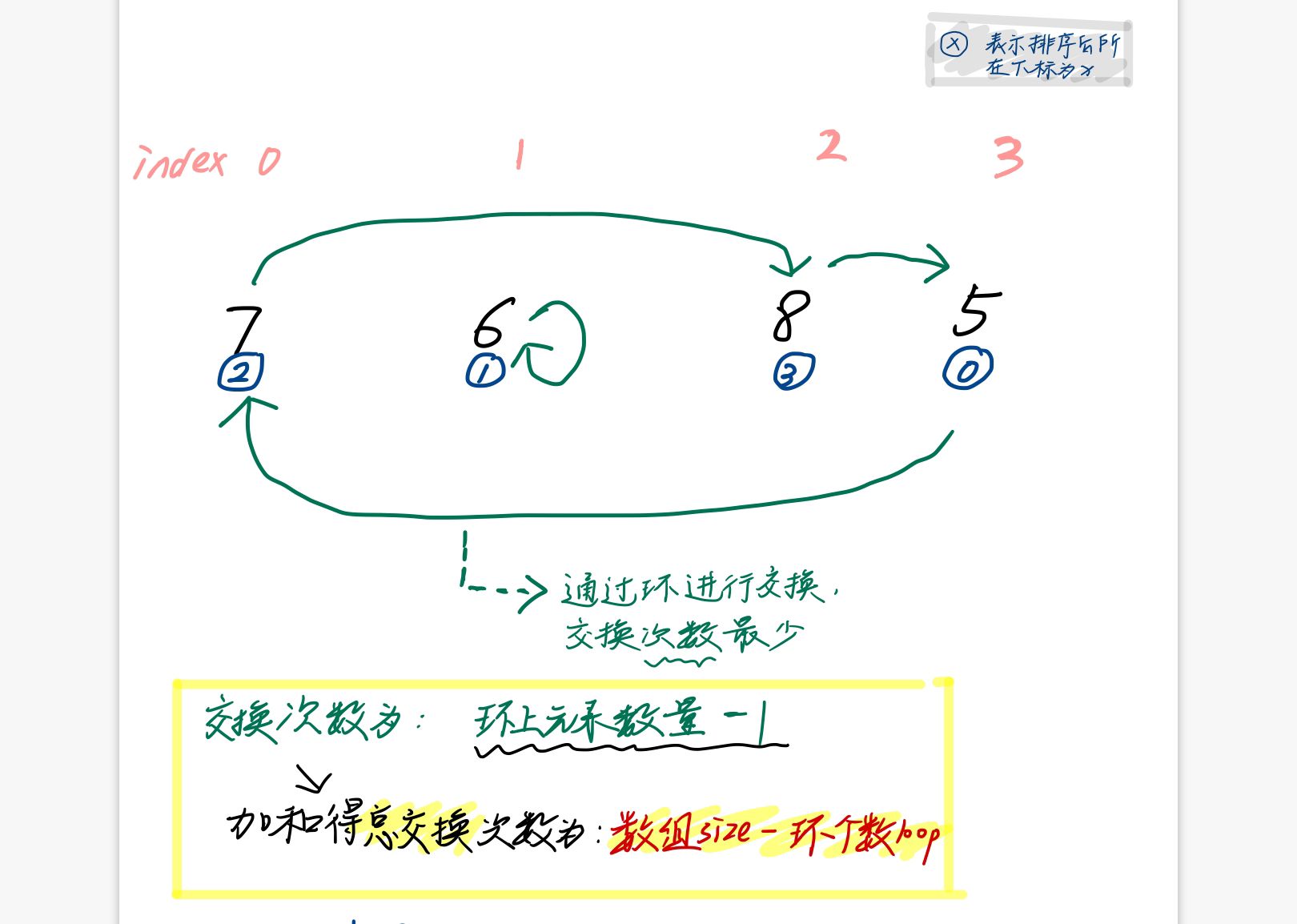
使用置换环算法得到数组排序需要的最小交换次数。
具体实现思想:
- 使用Map记录每个节点值及其应该放到的位置
- 从头到尾遍历初始数组,使用flag[]数组标记当前元素是否已经参与过(即已经被加入环中),对已经参与过的数组则不再需要遍历。每次成环结束,记录成环个数loop。
- 最终最小交换次数为:数组长度-成环个数 nums.size()-loop
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| // 返回使得 nums 递增需要的最小交换元素次数
public int minChanges(int[] nums){
int[] copy = Arrays.copyOf(nums, nums.length);
Arrays.sort(copy);
HashMap<Integer, Integer> map = new HashMap<>();
for(int i=0; i<copy.length; i++){
map.put(copy[i], i);
}
boolean[] flag = new boolean[nums.length]; // 用于标记 nums[i] 是否已经被加入环中
int loop = 0; // 环的个数
for(int i=0; i<nums.length; i++){
if(!flag[i]){
int j = i;
while(!flag[j]){ // 画环
int index = map.get(nums[j]); // 当前节点指向的位置,画环过程
flag[j] = true; // 将 j 加入环中
j = index; // 将当前节点移动到环上下个节点
}
loop++; // 环数递增
}
}
return nums.length - loop; // 最小交换次数为 : 数组长度 - 环数
}
作者:晚晴🌤
链接:https://leetcode.cn/problems/minimum-number-of-operations-to-sort-a-binary-tree-by-level/solutions/1965867/by-liu-wan-qing-zjlj/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
|



